52. N皇后 II

之前的解法：点我

位运算解法：

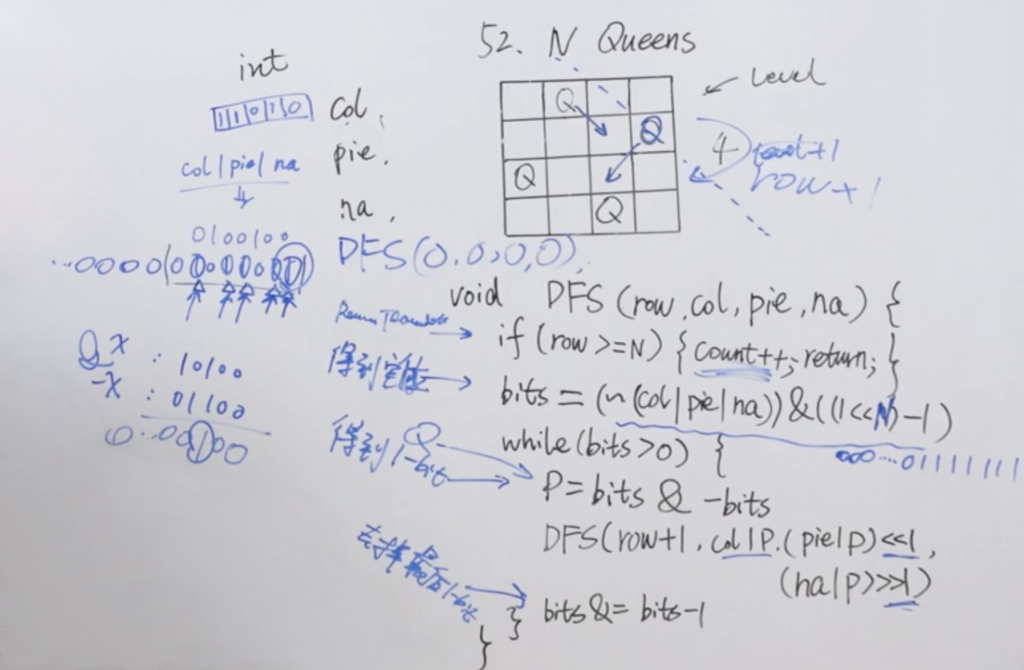
优化之前的三个 SET/数组，直接使用三个整数，通过位运算进行判断。

具体实现：使用 int 的二进制位是否为1作为是否存放了皇后的标记。说句实在话，讲不太清楚。

这里涉及到好几个位运算。模板代码：

void DFS(row,col,pie,na){
    if(row >= N){
        count++
        return
    }
    bits = (~(col | pie | na) & ((1 << n) -1))
    while (bits > 0){
        P = bits & -bits
        DFS(row + 1, col | P, (pie | P)<<1, (na | P)>>1)
        bits = bits & (bits-1)
    }
}

其中 bits = (~(col | pie | na) & ((1 << n) -1)) 是为了找出当前可以放皇后的地方，得到有效的空位。col、pie、na以二进制位进行标记，放过的位置标记为1。

前半部分即~(col | pie | na)三种条件的”或运算”取反，会得到一个二进制数，特点是：标记为1的地方可以放置皇后（之前是放过的为1，取反后颠倒）。

后半部分& ((1 << n) -1) 是为了抹掉 n 位之前的那些1（因为 col 等高位都是0，取反后高位就都成了1，但棋盘大小只有 n，所以后 n 位之前的都应该被处理成0）。

对应白板位置：

while (bits > 0) 代表：只要有空位就继续搜索。

P = bits & -bits 代表： 获取空位中的 1 ，用于给到col、pie、na 进行下一层的递归。

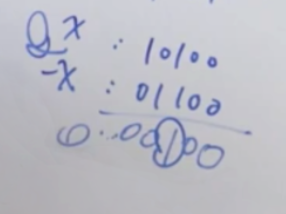
DFS(row + 1, col | P, (pie | P) << 1, (na | P) >> 1) ：将上一步得到的1，也就是放置的皇后位置用或运算记录到 col、pie、na，同时 pie、na 分别左移（因为 row+1，所以是实际上往左下移一格）和右移（同理右下移一格）来对齐到对角线的格子，继续递归。

bits = bits & (bits – 1) 代表：递归的回溯操作，将放置过的皇后一一消除，也就是每一层都消除最后的那个1。

class Solution {
    private var count = 0

    fun totalNQueens(n: Int): Int {
        if (n == 0) return count
        backtrack(n, 0, 0, 0, 0)
        return count
    }

    private fun backtrack(n: Int, row: Int, col: Int, pie: Int, na: Int) {
        if (row == n) {
            count++
            return
        }
        //得到有效的空位
        var bits = (col or pie or na).inv() and (1.shl(n) - 1)
        //一直循环到无空位
        while (bits > 0) {
            //得到一个空位
            val p = bits and -bits
            //占领这个空位并递归
            backtrack(n, row + 1, col or p, (pie or p).shl(1), (na or p).shr(1))
            //退回空位并回溯
            bits = bits and (bits - 1)
        }
    }
}

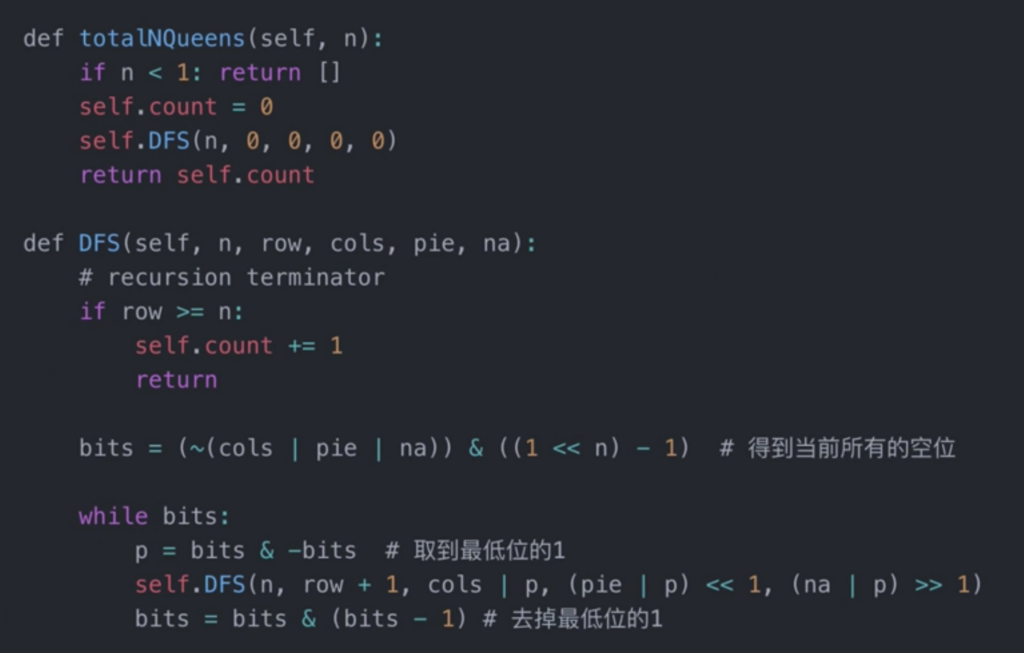
看下老师的 Python 版：