四点关键:
- 递归+记忆化 —> 递推
- 状态的定义:opt[n], dp[n], fib[n]
- 状态转移⽅程:opt[n] = best_of(opt[n-1], opt[n-2], …)
- 最优子结构
所谓规划实际上是指递推,可用递归+记忆化推导出递推,不存在规划,不会有什么远至10年后的高瞻远瞩。
例1:剑指 Offer 10- I. 斐波那契数列
0, 1, 1, 2, 3, 5, 8, 13, 21, …
递推公式:F[n] = F[n-1] + F[n-2]
递归图解:
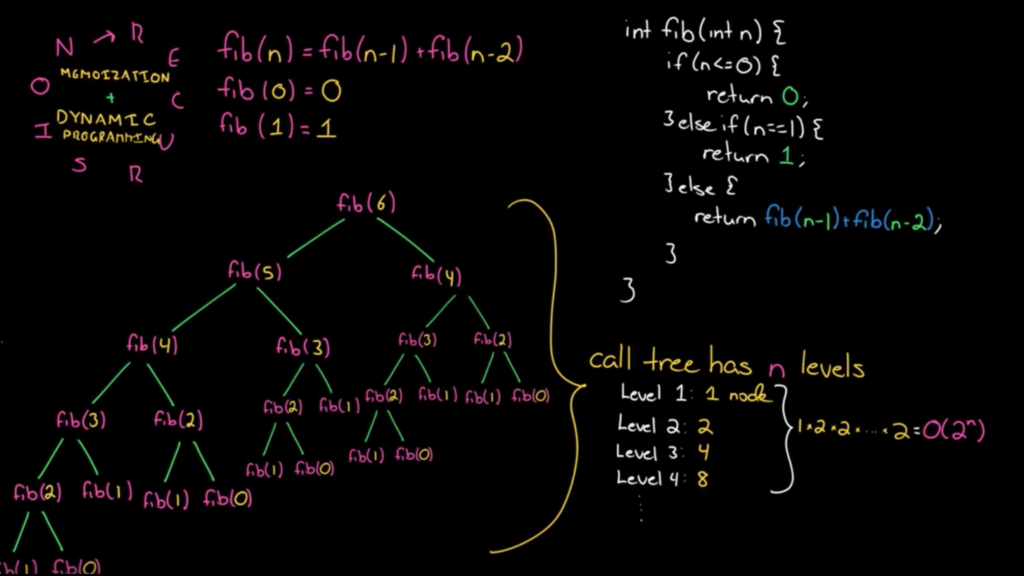
fun fib(n: Int): Int {
if (n <= 1) {
return n
}
return fib(n - 1) + fib(n - 2)
}这个的问题在于分支太多,时间复杂度为2的 n 次方。需要优化,可以颠倒顺序,从下往上计算:

此时可以看到,从下往上的递推少了很多重复计算。
fun fib(n: Int): Int {
if (n <= 1) {
return n
}
val f = IntArray(n+1)
f[0] = 0
f[1] = 1
for (i in 2..n) {
f[i] = (f[i - 1] + f[i - 2]) % 1000000007
}
return f[n]
}这里实际上也不需要用数组,只需要保存两个变量即可。
fun fib(n: Int): Int {
if (n <= 1) return n
var pre = 0
var cur = 1
for (i in 2..n) {
val res = ( pre + cur ) % 1000000007
pre = cur
cur = res
}
return cur
}这里的%操作:看这个回答,为什么很多程序竞赛题目都要求答案对 1e9+7 取模?
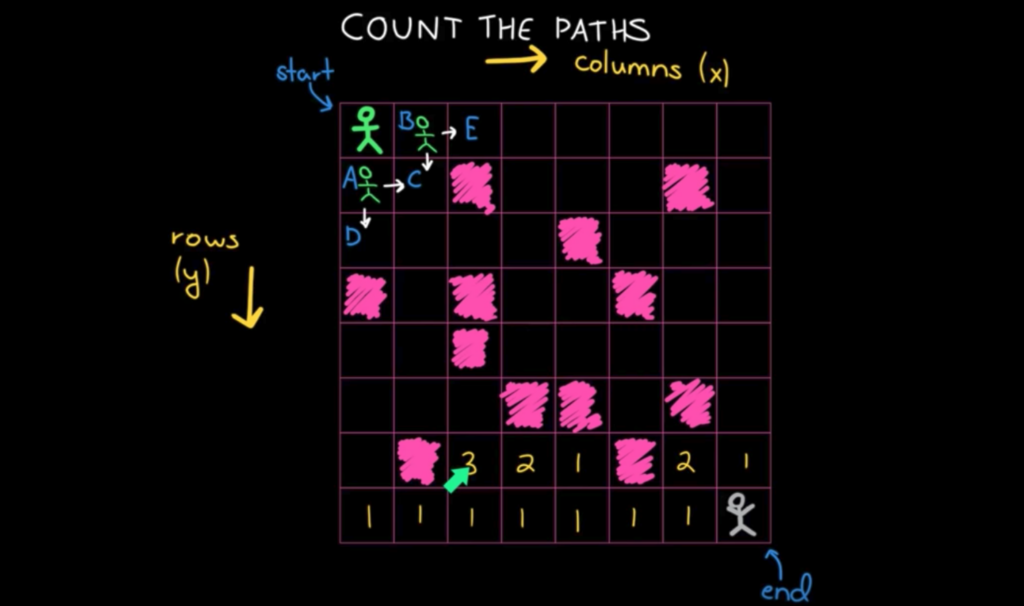
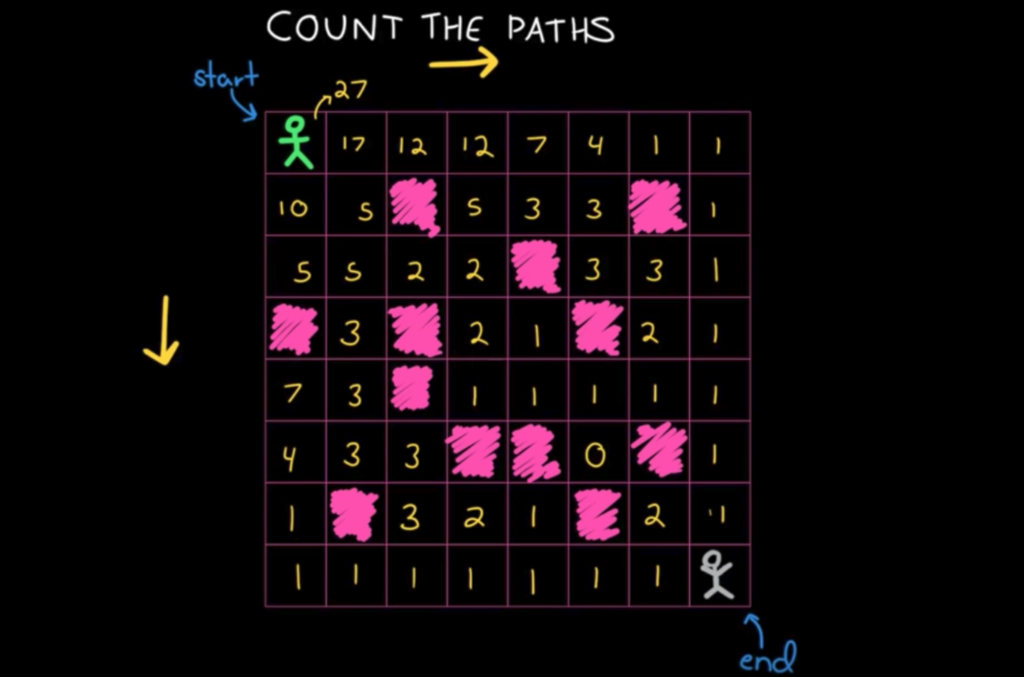
例2:查找路径和
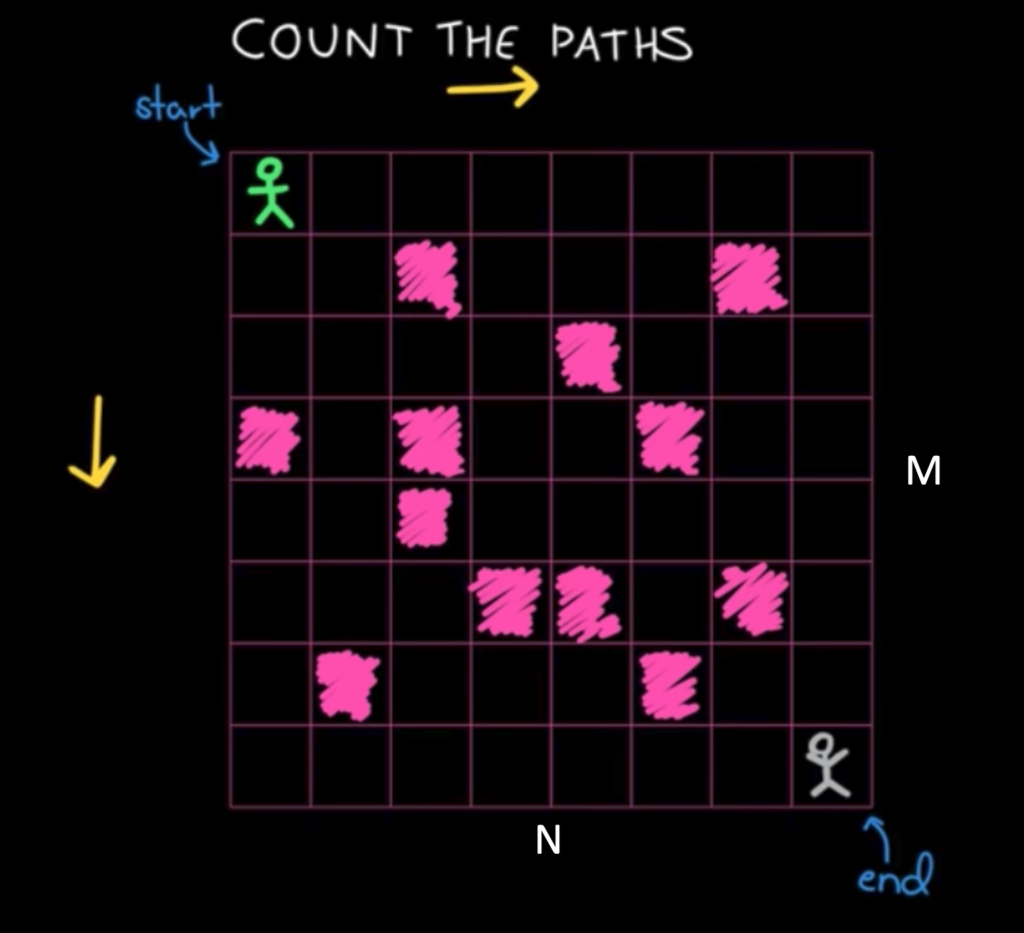

看上去很复杂,但实际上每次也只需要走一步,和斐波拉契类似。那么优化下走法,从确定的元素开始推导。也就是从右下角开始,路径(状态)都是确定的。
递归一般是从上至下,递推一般是从下至上,从确定状态到不确定状态。递推的状态一般是相邻的。
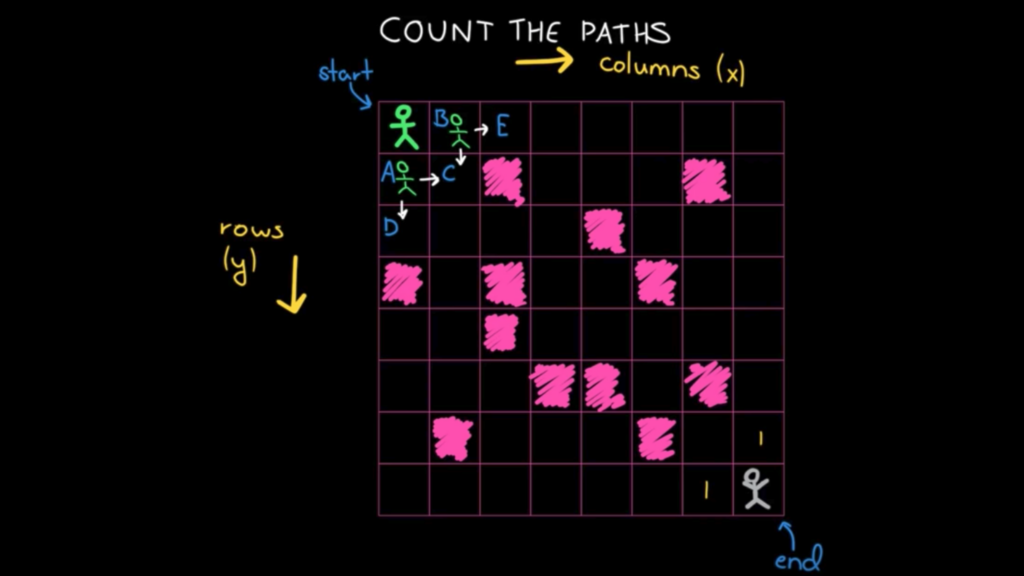
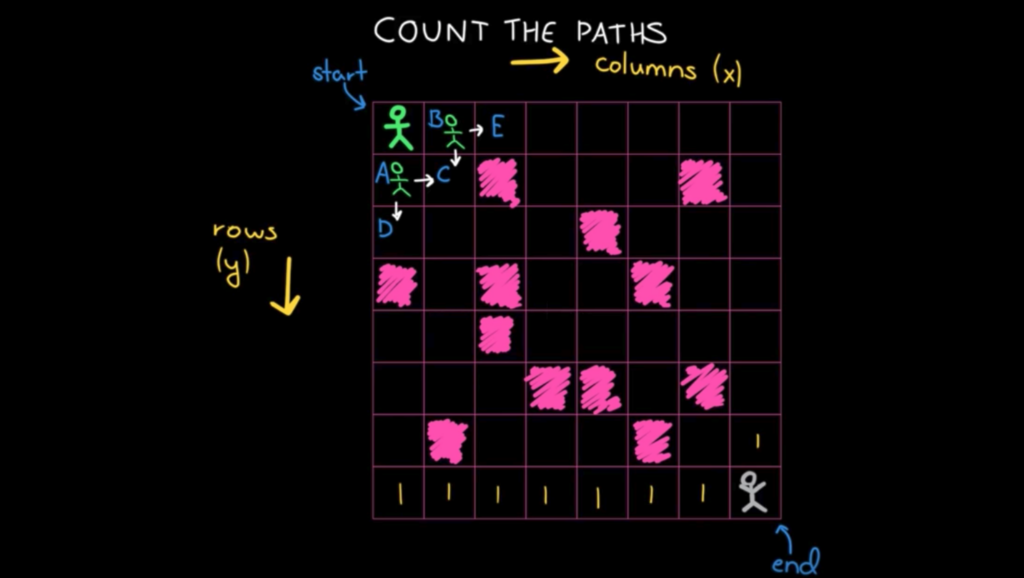
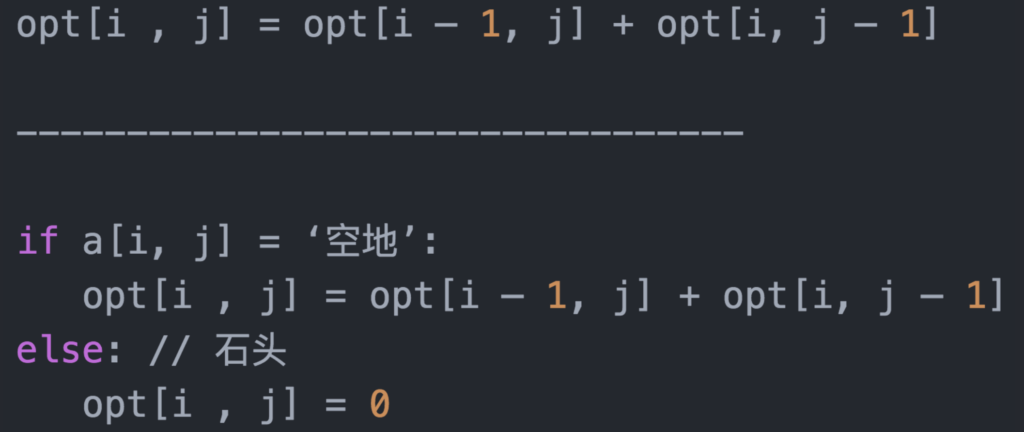
递推公式:
动态规划 vs 回溯 vs 贪⼼心算法
- 回溯(递归)— 重复计算
- 贪⼼算法 — 永远局部最优
- 动态规划 — 记录局部最优⼦结构 / 多种记录值
实战题目:
看题目就知道,这个章节挺猛的。
本站由以下主机服务商提供服务支持:
0条评论