547. 朋友圈

按题目思路分析后，实际上也是一个并查集的问题

1. 对角线没有意义，因为是自己认识自己
2. 相邻则可以合为一个并集

即：看有多少个并查集，多少个 root

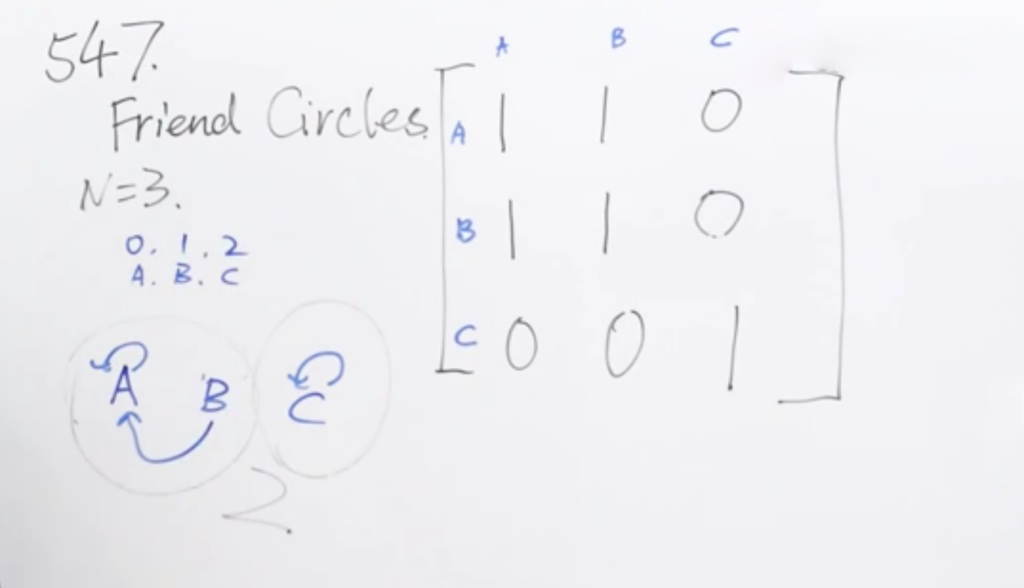
老师说与上一节的代码类似，我写了下:

class Solution {

    fun findCircleNum(M: Array<IntArray>): Int {
        if (M.isNullOrEmpty()) return 0
        if (M[0].isEmpty()) return 0

        val m = M.size
        val n = M[0].size

        val uf = UnionFind(M)

        for (i in 0 until m) {
            for (j in 0 until n) {
                if (M[i][j] == 0) continue
                if (M[i][j] == 1) uf.union(i, j)
            }
        }
        
        return uf.count
    }

    class UnionFind(grid: Array<IntArray>) {

        val m = grid.size
        var count = 0
        //初始化为自身或者初始化为-1都没关系
        val parent = IntArray(m) { it }

        //用于深度合并优化
        val rank = IntArray(m) { 0 }

        init {
            for (i in 0 until m) {
                parent[i] = i
                count++
            }
        }

        fun findRoot(p: Int): Int {
            if (parent[p] != p) {
                parent[p] = findRoot(parent[p])
            }
            return parent[p]
        }

        fun union(x: Int, y: Int) {
            val rootX = findRoot(x)
            val rootY = findRoot(y)
            if (rootX != rootY) {
                when {
                    rank[rootX] > rank[rootY] -> {
                        parent[rootY] = rootX
                    }
                    rank[rootX] > rank[rootY] -> {
                        parent[rootX] = rootY
                    }
                    else -> {
                        parent[rootY] = rootX
                        rank[rootX]++
                    }
                }
                count--
            }
        }

    }

}

上面的写法还可以再优化一下：因为是对称矩阵

class Solution {

    fun findCircleNum(M: Array<IntArray>): Int {
        if (M.isNullOrEmpty()) return 0
        if (M[0].isEmpty()) return 0

        val n = M.size
        val uf = UnionFind(n)

        for (i in 0 until n) {
            for (j in 0 until i) {
                if (M[i][j] == 0) continue
                if (M[i][j] == 1) uf.union(i, j)
            }
        }

        return uf.count
    }

    class UnionFind(n: Int) {

        var count = 0
        //初始化为本身 或者为-1都没关系
        val parent = IntArray(n) { it }

        //用于深度合并优化
        val rank = IntArray(n) { 0 }

        init {
            for (i in 0 until n) {
                parent[i] = i
                count++
            }
        }

        fun findRoot(p: Int): Int {
            if (parent[p] != p) {
                parent[p] = findRoot(parent[p])
            }
            return parent[p]
        }

        fun union(x: Int, y: Int) {
            val rootX = findRoot(x)
            val rootY = findRoot(y)
            if (rootX != rootY) {
                when {
                    rank[rootX] > rank[rootY] -> {
                        parent[rootY] = rootX
                    }
                    rank[rootX] > rank[rootY] -> {
                        parent[rootX] = rootY
                    }
                    else -> {
                        parent[rootY] = rootX
                        rank[rootX]++
                    }
                }
                count--
            }
        }

    }

}

发现，还是官方的这个解法看上去更简单：

官方的思路是：先来一个并查集，将parent 都填充为 -1，每联接一个元素则那个元素将不再是 -1，最后统计 -1 的个数。

并查集的大小为 N 是因为当每个人都是单独的朋友圈时最多，大小 N 个。

class Solution {
    fun find(parent: IntArray, i: Int): Int {
        return if (parent[i] == -1) i else find(parent, parent[i])
    }

    fun union(parent: IntArray, x: Int, y: Int) {
        val xset = find(parent, x)
        val yset = find(parent, y)
        if (xset != yset) parent[xset] = yset
    }

    fun findCircleNum(M: Array<IntArray>): Int {
        val parent = IntArray(M.size)
        Arrays.fill(parent, -1)
        for (i in M.indices) {
            for (j in M.indices) {
                if (M[i][j] == 1 && i != j) {
                    union(parent, i, j)
                }
            }
        }
        var count = 0
        for (i in parent.indices) {
            if (parent[i] == -1) count++
        }
        return count
    }
}

然后这题，DFS也是可以的：以下是官方的代码

思路是：从一个没有被访问的同学开始，找这个同学所在的行有没有认识的，有认识的话，就把这一列扫一遍，过滤掉没有被访问过的元素，同时把朋友的朋友记录下来，最后回去一开始，继续从未被访问的开始访问，每一次深度递归的开始都是一个新的朋友圈。

class Solution {
    fun dfs(M: Array<IntArray>, visited: IntArray, i: Int) {
        for (j in M.indices) {
            if (M[i][j] == 1 && visited[j] == 0) {
                visited[j] = 1
                dfs(M, visited, j)
            }
        }
    }

    fun findCircleNum(M: Array<IntArray>): Int {
        val visited = IntArray(M.size)
        var count = 0
        for (i in M.indices) {
            if (visited[i] == 0) {
                dfs(M, visited, i)
                count++
            }
        }
        return count
    }
}

有 DFS 那么 BFS 也就有了。

class Solution {
    fun findCircleNum(M: Array<IntArray>): Int {
        val visited = IntArray(M.size)
        var count = 0
        val queue = LinkedList<Int>()
        for (i in M.indices) {
            if (visited[i] == 0) {
                queue.add(i)
                while (!queue.isEmpty()) {
                    val s = queue.pop()
                    visited[s] = 1
                    for (j in M.indices) {
                        if (M[s][j] == 1 && visited[j] == 0) queue.add(j)
                    }
                }
                count++
            }
        }
        return count
    }
}