题目一：

703. 数据流中的第K大元素

解法一：简化问题，如果只是找最大的元素，那么每次进入一个元素，就与之前的最大值进行判断即可，意味着只保留一个最大值。

那么第 K 大的元素，就保存 K 个值，每进来一个就与 K 个中最小的进行比较，同时保持 K 个元素，那么如何保证是最大的 K 个元素呢？

最简单直接的办法：排序，这里肯定是选快排，直接对前 K 个最大与新进入的元素进行整个排序，把最小的淘汰掉。

时间复杂度 :O(N * K * logK) = N 个元素 * 每次 K 个元素的排序

解法二：使用优先队列，把最大的放最上面，或者把最小的放最上面。

这里使用使用小顶堆，堆大小为 K，优先级从小到大，每次进入时与堆顶进行对比，小于堆顶则可直接丢弃，大于则剔除之前堆顶元素，放入堆重新维护。

关于这个方法，推荐一篇文章：https://juejin.im/post/5c0b75fef265da6115109d35

时间复杂度：N 次运算O(N) * 新进元素只用判断一次，舍弃状态的 O(1) or 需要多次判断的调整的 O(log₂K)

所以最优是：O(N *1) 最差是：O(N*log₂K)，平均取最大值O(N*log₂K)

总结：对于流式数据一个一个元素进入，则可以省去前面的 N，则解法二O(log₂K)优于解法一O(K * logK)。

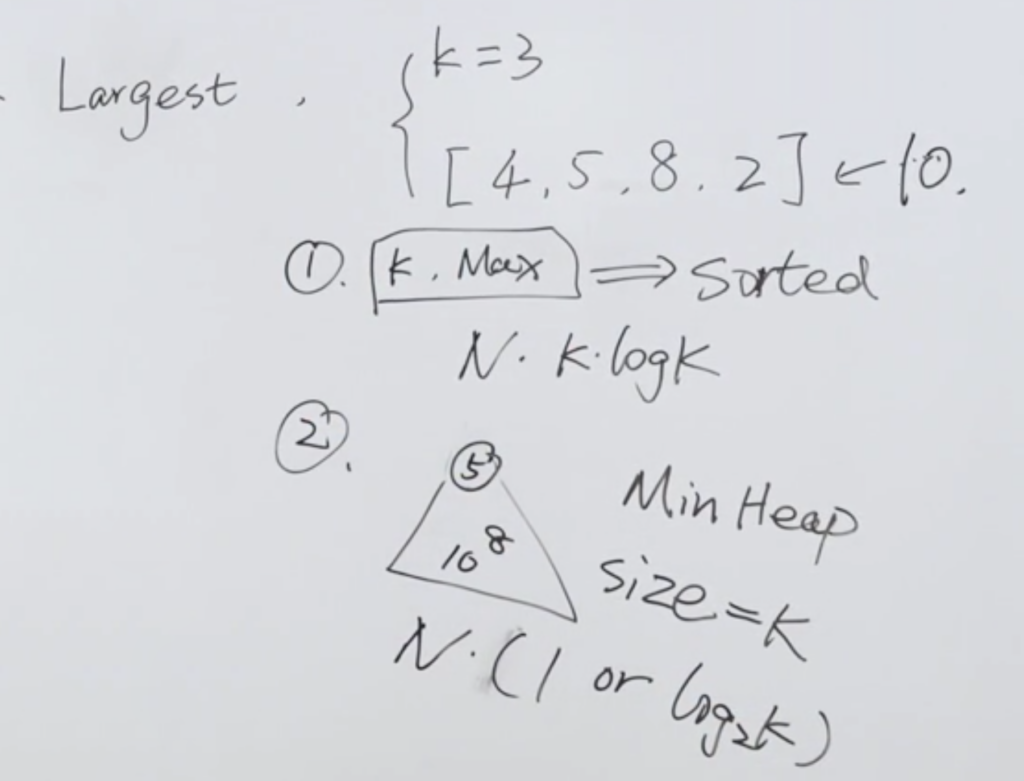
题目二：

239. 滑动窗口最大值

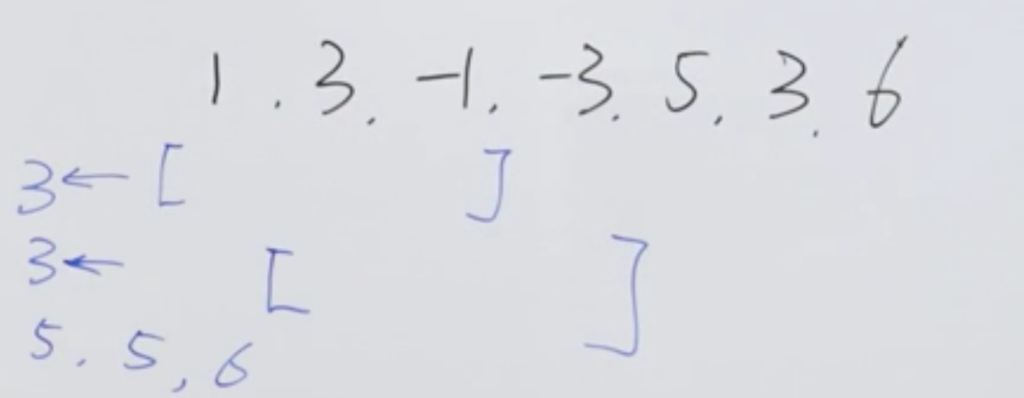
解法一：优先队列解法

由于是找最大值，所以使用大顶堆，移动时维护堆，删除离开的元素，加入新的元素，并调整堆，此时结果就是堆顶元素。

时间复杂度：O(N * logK) = N 个元素 * 维护O(logK) * 查找O(1)

解法二：分析特点，每次只有三个元素，大小有限，所以简化解法一，直接使用双端队列deque，维护队列。（标准解法）

队列的维护时思想：维护最大值永远为最左边的值。

移动时进入的数字如果小于最左边元素同时队列未满，则填充队列。若大于最左边的元素（最大值），则移除队列中所有元素，只保留当前新加入元素。注意队列只存数组下标。

时间复杂度：O(N * 1) = N 个元素 O(N) * 每个元素在窗口中只走一个过场，此时查询的复杂度是 O(1)

其他解法：https://leetcode-cn.com/problems/sliding-window-maximum/solution/hua-dong-chuang-kou-zui-da-zhi-by-leetcode-3/