50. Pow(x, n)

解法一：直接使用系统函数。

时间复杂度：O(1)

解法二：暴力，for 循环。

时间复杂度：O(N)

解法三：分治，整个分两边，考虑奇偶

偶数时：结果=X^n/2 * X^n/2

奇数时：结果=X^(n – 1)/2 * X^(n – 1)/2 * X，同时由于是取整，所以是：X^n/2 * X^n/2 * X

一直拆分下去，时间复杂度： O(logN)

这个更清楚，leetcode 题解：50. Pow(x, n) （快速幂，清晰图解）

递归版：

class Solution {
    fun myPow(x: Double, n: Int): Double {
        //终止条件
        if (n == 0) return 1.0
        if (n == 1) return x
        if (n == -1) return 1/x
        val half = myPow(x, n / 2)
        val rest = myPow(x, n % 2)
        return rest * half * half
    }
}

非递归版：注意这里转 Long 不是没有原因的，超出限制了。

上面题解中的一张图很适合这份代码：

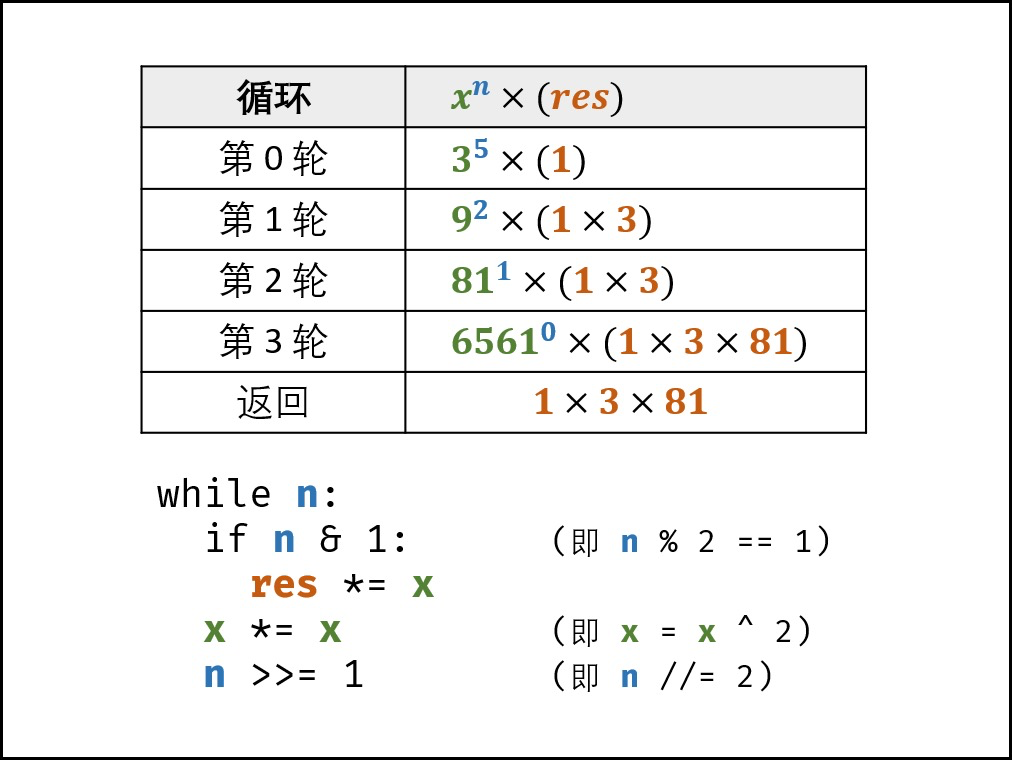
在这份代码中，当 n 为奇数时，会先乘上一个 x，最后再存下结果，n 为偶数时，只会在最后存在结果。这部分代码解决了奇偶性条件问题，而且这代码位置摆放得也很妙。

if (times % 2 == 1L) res *= num

class Solution {
    fun myPow(x: Double, n: Int): Double {
        var times = n.toLong()

        if (x == 0.0) return x

        var num = x

        if (times < 0) {
            num = 1 / num
            times *= -1
        }
        var res = 1.0
        while (times > 0) {
            if (times % 2 == 1L){
                res *= num
            }
            num *= num
            times /= 2
        }
        return res
    }
}