102. 二叉树的层序遍历

解法一：BFS

直接遍历，直接存放，一层一层放完。

判断当前层已结束的两种方法：

1. 将当前层数保存到队列中（不推荐）
2. Beetch process（代码中体现）

时间复杂度：O(N)

fun levelOrder(root: TreeNode?): ArrayList<ArrayList<Int>> {
    val res = ArrayList<ArrayList<Int>>()
    root ?: return res

    val q = LinkedList<TreeNode>()
    q.add(root)

    while (q.isNotEmpty()) {
        val levelSize = q.size
        val currentLevel = ArrayList<Int>()

        for (i in 0 until levelSize) {
            val curNode = q.poll()
            currentLevel.add(curNode.`val`)
            curNode.left?.also {
                q.add(it)
            }
            curNode.right?.also {
                q.add(it)
            }
        }
        res.add(currentLevel)
    }
    return res
}

解法二：DFS 也可

深度遍历，按层填充，逐渐放完。

时间复杂度：O(N)

递归写法：

fun levelOrder(root: TreeNode?): ArrayList<ArrayList<Int>> {
    val res = ArrayList<ArrayList<Int>>()
    root ?: return res
    dfs(root, res, 0)
    return res
}

private fun dfs(node: TreeNode?, res: ArrayList<ArrayList<Int>>, level: Int) {
    node ?: return
    //预先建立坑位
    if (res.size - 1 < level) {
        res.add(ArrayList())
    }
    //直接使用坑位
    res[level].add(node.`val`)

    dfs(node.left, res, level + 1)
    dfs(node.right, res, level + 1)
}

非递归写法：问了大佬，确实有解

class Solution {
    fun addNode(res: ArrayList<ArrayList<Int>>, node: Pair<TreeNode?, Int>) {
        if (res.size == 0 || node.second + 1 > res.size) {
            for (i in 0 until node.second + 1 - res.size) {
                res.add(ArrayList())
            }
        }
        res[node.second].add(node.first!!.`val`)
    }

    fun levelOrder(root: TreeNode?): ArrayList<ArrayList<Int>> {
        val res = ArrayList<ArrayList<Int>>()
        val stack = Stack<Pair<TreeNode?, Int>>()
        var cur = Pair(root, 0)
        while (cur.first!=null || stack.isNotEmpty()) {
            while (cur.first !=null) {
                addNode(res, cur)
                val node = cur.first
                stack.push(Pair(node!!.right, cur.second + 1))
                cur = Pair(node.left, cur.second + 1)
            }
            cur = stack.pop()
        }
        return res
    }

}

两种方法都还好，不好理解的话，配合断点调试食用。如果是图的遍历，需加上 visited 判断。

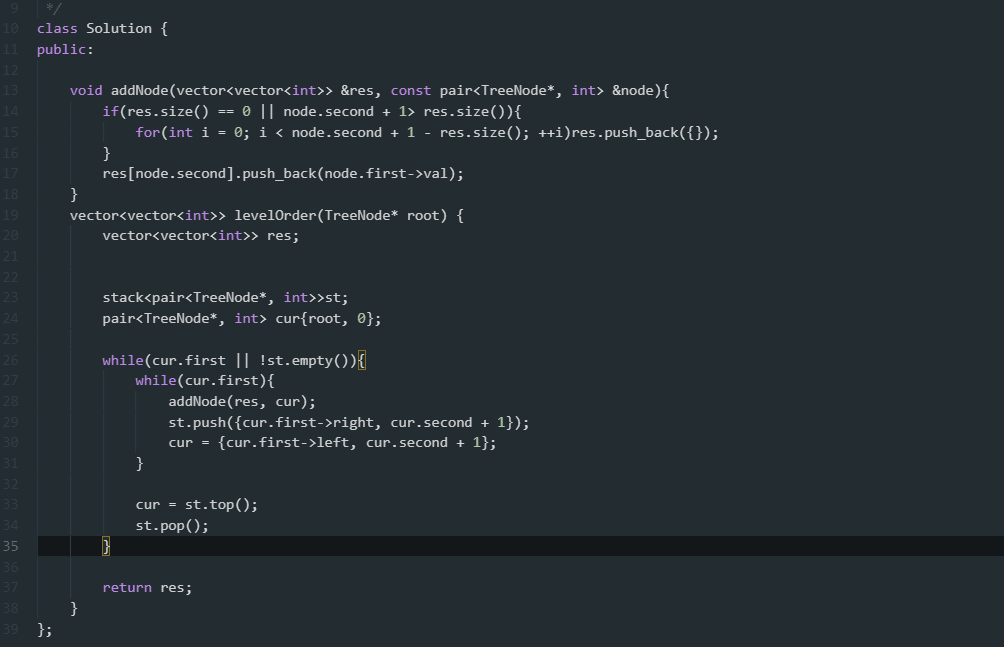
附上大佬的 C++原版，或许有人用得着：