104. 二叉树的最大深度

解法一：DFS递归

时间复杂度：O(N)

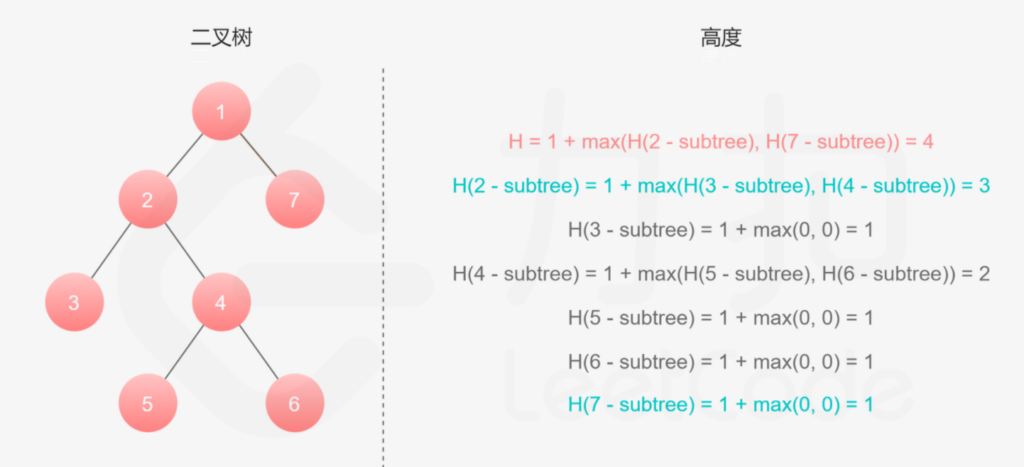
图解：来自leetcode 官方

/**
 * Example:
 * var ti = TreeNode(5)
 * var v = ti.`val`
 * Definition for a binary tree node.
 * class TreeNode(var `val`: Int) {
 *     var left: TreeNode? = null
 *     var right: TreeNode? = null
 * }
 */
class Solution {
    fun maxDepth(root: TreeNode?): Int {
        root ?: return 0
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
    }
}

解法二：DFS非递归

保存一个值 max 用于记录level深度，每次遍历时遇到叶子节点与 max 值进行比较，大于 max 则更新 max即可。

时间复杂度：O(N)

class Solution {
    fun maxDepth(root: TreeNode?): Int {
        root ?: return 0
        var max = Int.MIN_VALUE
        val stack = Stack<Pair<TreeNode?, Int>>()
        var cur = Pair<TreeNode?, Int>(root, 0)
        while (cur.first != null || stack.isNotEmpty()) {
            while (cur.first != null) {
                if (cur.first!!.left == null && cur.first!!.right == null) {
                    max = Math.max(max, cur.second + 1)
                }

                val node = cur.first
                stack.push(Pair(node!!.right, cur.second + 1))
                cur = Pair(node.left, cur.second + 1)
            }
            cur = stack.pop()
        }
        return max
    }
}

解法三：BFS

由于是按层扫描，最后一层就是最大深度。

时间复杂度：O(N)

class Solution {
    fun maxDepth(root: TreeNode?): Int {
        root ?: return 0

        var res = 0
        val q = LinkedList<TreeNode>()
        q.add(root)

        while (q.isNotEmpty()) {
            val levelSize = q.size
            for (i in 0 until levelSize) {
                val curNode = q.poll()
                curNode.left?.also {
                    q.add(it)
                }
                curNode.right?.also {
                    q.add(it)
                }
            }
            res++
        }
        return res
    }
}

111. 二叉树的最小深度

解法一：DFS递归

需要注意的是特殊情况，没有左子树的时候与没有右子树的时候。

时间复杂度：O(N)

/**
 * Example:
 * var ti = TreeNode(5)
 * var v = ti.`val`
 * Definition for a binary tree node.
 * class TreeNode(var `val`: Int) {
 *     var left: TreeNode? = null
 *     var right: TreeNode? = null
 * }
 */
class Solution {
    fun minDepth(root: TreeNode?): Int {
        root ?: return 0
        root.left ?: return 1 + minDepth(root.right)
        root.right ?: return 1 + minDepth(root.left)

        val minL = minDepth(root.left)
        val minR = minDepth(root.right)

        return Math.min(minL, minR) + 1
    }
}

简化版本：主要是return 时增加了情况覆盖

class Solution {
    fun minDepth(root: TreeNode?): Int {
        root ?: return 0
        val minL = minDepth(root.left)
        val minR = minDepth(root.right)
        return if (minL == 0 || minR == 0) {
            minL + minR + 1
        } else {
            Math.min(minL, minR) + 1
        }
    }
}

解法二：DFS非递归

保存一个值 min 用于记录level深度，每次遍历时遇到叶子节点与 min 值进行比较，小于 min 则更新 min即可。

时间复杂度：O(N)

class Solution {
    fun minDepth(root: TreeNode?): Int {
        root ?: return 0
        var min = Int.MAX_VALUE
        val stack = Stack<Pair<TreeNode?, Int>>()
        var cur = Pair<TreeNode?, Int>(root, 0)
        while (cur.first != null || stack.isNotEmpty()) {
            while (cur.first != null) {
                if (cur.first!!.left == null && cur.first!!.right == null) {
                    min = Math.min(min, cur.second + 1)
                }

                val node = cur.first
                stack.push(Pair(node!!.right, cur.second + 1))
                cur = Pair(node.left, cur.second + 1)
            }
            cur = stack.pop()
        }
        return min
    }
}

解法三：BFS

由于是按层扫描，那么扫描时判断是否是叶子节点即可。

时间复杂度：O(N)

class Solution {
    fun minDepth(root: TreeNode?): Int {
        root ?: return 0

        var level = 0
        val q = LinkedList<TreeNode>()
        q.add(root)

        while (q.isNotEmpty()) {
            val levelSize = q.size
            for (i in 0 until levelSize) {
                val curNode = q.poll()
                curNode.left?.also {
                    q.add(it)
                }
                curNode.right?.also {
                    q.add(it)
                }

                if (curNode.left == null && curNode.right == null) {
                    return ++level
                }
            }
            level++
        }
        return level
    }
}