51. N皇后

解法：搜索，DFS递归

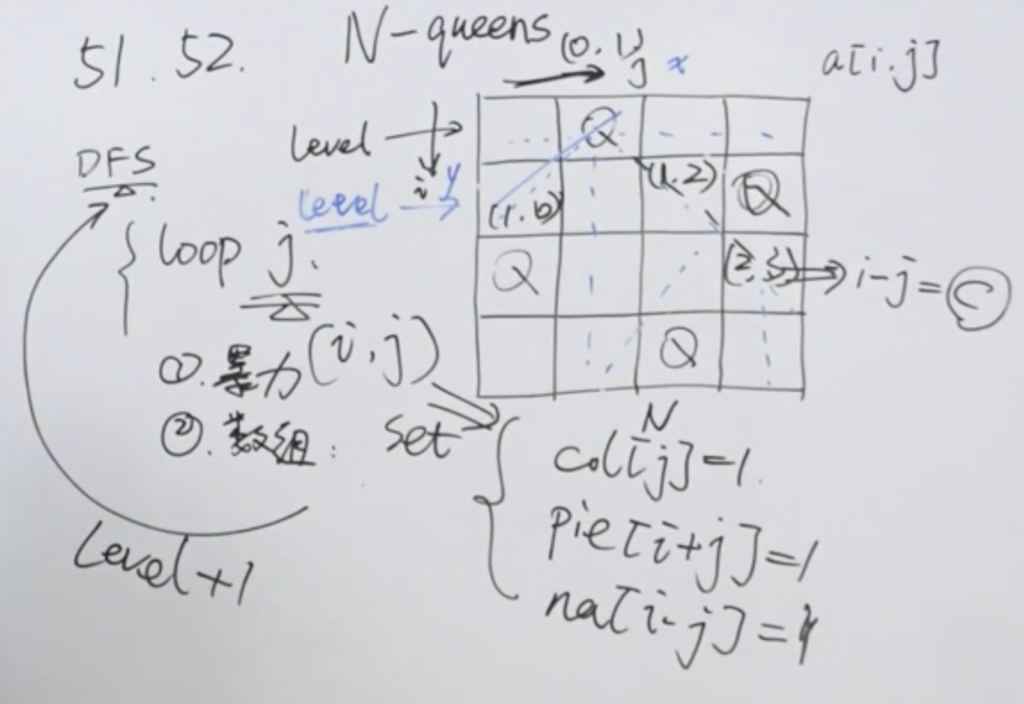
思路：每层递归，枚举每一列，确认皇后放置位置。判断格子能不能放有两种方式：

1. 暴力 把整个盘都扫一遍。
2. 剪枝，用缓存将已经存在的位置保存下来。

保存位置可使用数组row[i]，clown[j]，但行 row[i]可以不用管，因为这里 DFS 是按层递归。此外正反两个对角线分别满足规律（c 是一个常数）：i + j = c 与 i – j = c

存放对角线冲突位置时，可选数组/Set，选用数组时需做变换，因不能为负数。选用 SET 则无需处理。

写一个 DFS，遍历每层，判断当前的 i，j 是否在以上条件之外，即不存在攻击。满足后将当前i，j 位置的 列以及对角常数 c 缓存，用于下次冲突判断。随后 level ++。

注意：无论有没有找到都需要重置场景（进行回溯）。

关于回溯，不太明白的话看看官方题解中回溯部分的步骤图，一张一张往下看，会知道为什么要重置场景，也会知道为什么叫回溯。其实就是推翻重来，以此找寻所有可能性。

时间复杂度：空间换时间，接近于 O(N!)，关于 N 皇后的复杂度网上有很多描述，这里参考 leedcode 官方题解（极客时间这节的时间复杂度并没说明白，只说当 n 大于20时便很糟糕了，指数级。）

代码：总算找到一篇可借鉴的题解了 参考第一份代码的第二个 Java 版本

class Solution {
    private var res = ArrayList<List<String>>()

    private var colss = HashSet<Int>()
    private var xySum = HashSet<Int>()
    private var xyDiff = HashSet<Int>()

    fun solveNQueens(n: Int): List<List<String>> {
        if (n == 0) return res

        val stack = Stack<Int>()
        backtrack(n, 0, stack)
        return res
    }

    private fun backtrack(n: Int, row: Int, stack: Stack<Int>) {
        if (row == n) {
            res.add(convertBoard(stack, n))
            return
        }
        for (col in 0 until n) {
            if (col !in colss && row + col !in xySum && row - col !in xyDiff) {
                stack.add(col)

                colss.add(col)
                xySum.add(row + col)
                xyDiff.add(row - col)

                backtrack(n, row + 1, stack)

                xyDiff.remove(row - col)
                xySum.remove(row + col)
                colss.remove(col)

                stack.pop()
            }
        }
    }

    private fun convertBoard(stack: Stack<Int>, n: Int): List<String> {
        val board = ArrayList<String>()
        stack.forEach {
            val chars = CharArray(n)
            Arrays.fill(chars, '.')
            chars[it] = 'Q'
            board.add(String(chars))
        }
        return board
    }
}

同时还有一个同类型题，返回 size即可：

52. N皇后 II

fun totalNQueens(n: Int): Int {
    if (n == 0) return 0

    val stack = Stack<Int>()
    backtrack(n, 0, stack)
    return res.size
}

位运算版：这题本应该用位运算做，点我 。