37. 解数独

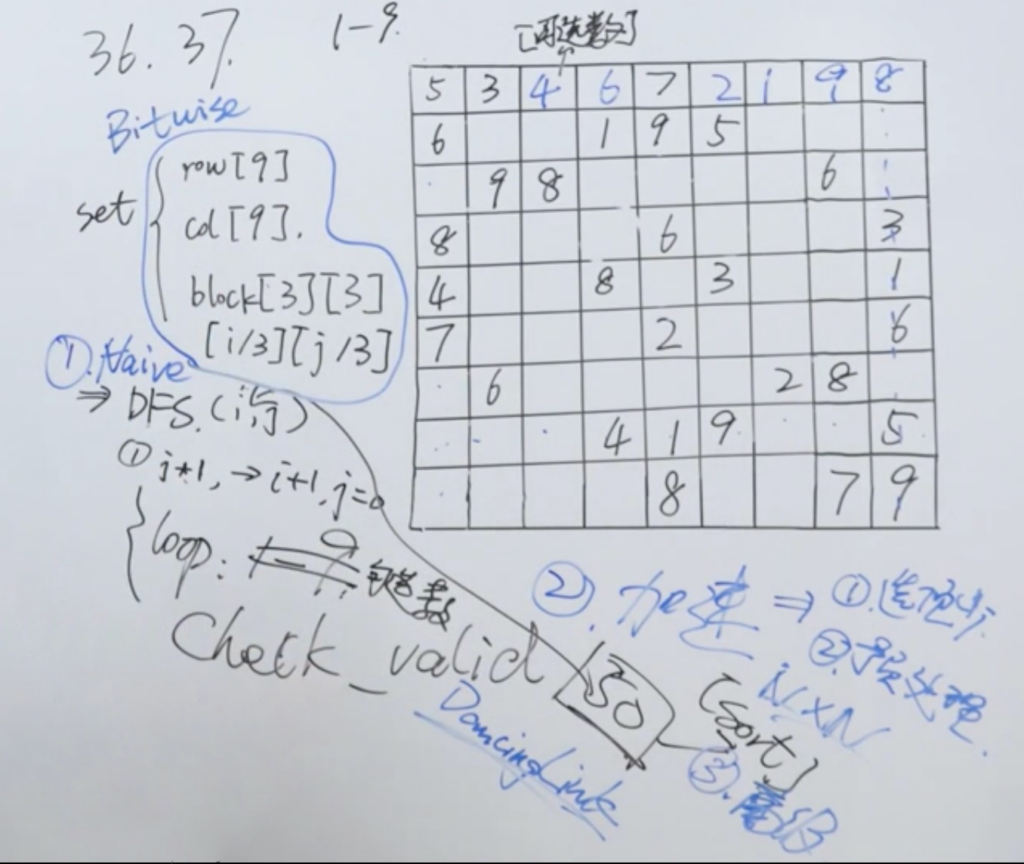
这题白板还确实有点复杂

数独的填充满足以下规律：

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

解法一：搜索

DFS，枚举每个空格，放入数字，判断是否合法，也就是是否满足上述3个规则。这是朴素搜索。

解法二：搜索 + 剪枝

人的思维：

先从已有数字多的行或者列开始，因为填的选项更少，所以回溯次数会减少。

转换为机器思维：

做预读，预处理，用 n*n 循环，扫一遍整个棋盘，把每个空位置的可选项存下来。再将可选数进行排序，从可选数少的位置开始 DFS 递归搜索，同时递归时不再是枚举1到9，而是枚举可选数，进一步压缩数据搜索范围。

解法三：高级数据结构

老师举例的是：DancingLink wiki

解法四：位运算

这节课老师还没讲到，后期看能不能补上。老师补了 N 皇后，位运算差不太多。但我并不熟，目前不打算补上。

解法有点多，复杂的涉及剪枝。只按老师的思路跑通了普通回溯版本：

class Solution {
    fun solveSudoku(board: Array<CharArray>): Unit {
        if (board.isNullOrEmpty()) return
        solve(board)
    }

    fun solve(board: Array<CharArray>): Boolean {
        for (row in board.indices)
            for (col in board[0].indices) {
                if (board[row][col] == '.') {
                    for (c in '1'..'9') {
                        if (isValid(board, row, col, c)) {
                            board[row][col] = c
                            if (solve(board))
                                return true
                            else
                                board[row][col] = '.'
                        }
                    }
                    return false
                }
            }
        return true
    }

    fun isValid(board: Array<CharArray>, row: Int, col: Int, c: Char): Boolean {
        for (i in 0 until 9) {
            if (board[i][col] != '.' && board[i][col] == c) return false
            if (board[row][i] != '.' && board[row][i] == c) return false
            if (board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] != '.'
                    && board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] == c) return false
        }
        return true
    }

}

还有一个简单版的：

36. 有效的数独

解法：写一个两层的循环，判断是否满足数独规则。

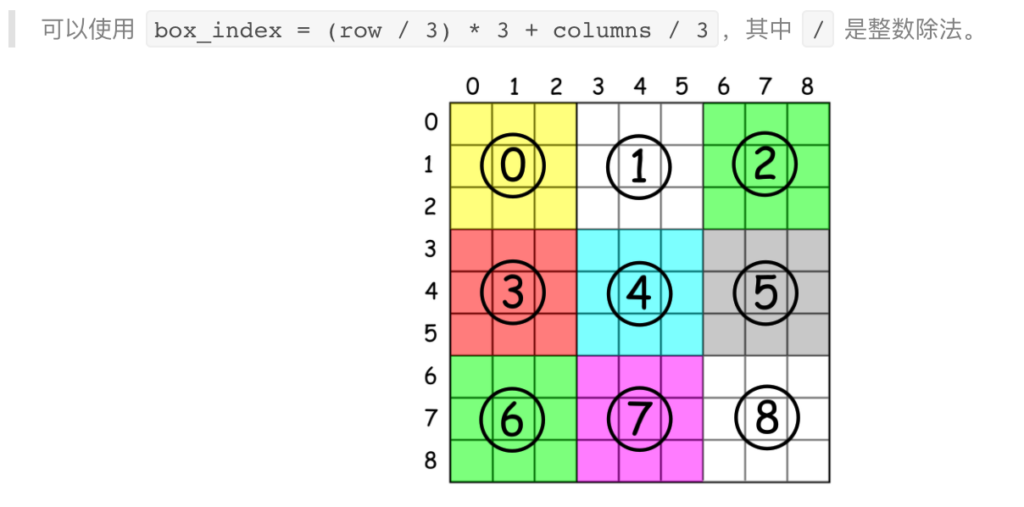
主要理解官方题解中的这部分，相信可以想明白：

class Solution {
    fun isValidSudoku(board: Array<CharArray>): Boolean {
        val rows = HashSet<String>()
        val columns = HashSet<String>()
        val boxes = HashSet<String>()

        for (row in board.indices) {
            for (col in board[0].indices) {
                val c = board[row][col]
                if (c != '.') {
                    val boxIndex = "${(row / 3) * 3 + col / 3}-$c"
                    val rowIndex = "$row-$c"
                    val colIndex = "$col-$c"
                    if (rowIndex in rows || colIndex in columns || boxIndex in boxes) {
                        return false
                    }
                    rows.add(rowIndex)
                    columns.add(colIndex)
                    boxes.add(boxIndex)
                }
            }
        }
        return true
    }
}