解法一:暴力递归
每个数都有两个选择,乘与不乘,乘则记录结果,不乘则从1重新开始。每次都要
得出一个 max,最后的 max,就是结果。
解法二:动态规划
- 状态定义:DP[ i ],从 开始 到 i 这个位置的最大值(并不一定是从0开始,而是最大值构成的范围开始),所以需要求 DP[ n – 1 ] DP[ n – 2 ] … DP[ 0 ]
- DP 方程:DP[ i + 1 ] = DP[ i ] * a[ i + 1 ] (前面一个的最大值 * 当前值)
也就是:DP[ i ] = DP[ i – 1 ] * a[ i ]
但这里有个问题,当 a[ i ] 为负的时候,DP[ i -1 ] 也需要是负数的最大值。所以,需要进行改进。
- 状态定义:DP[ i ][ 2 ],加一维,用于表示是正数还是负数,对应值:
0 – 正数max
1 – 负数min(负 max) - DP 方程:正负关系需要弄清楚
最大值 DP[ i , 0 ] :大于零:正 * 正。 小于零:负 * 负
if ( a[ i ] >= 0 ) { DP[ i – 1 , 0 ] * a[ i ] } else { DP[ i – 1 , 1 ] * a[ i ] }
最小值 DP[ i , 1 ] :大于零:负 * 正。 小于零:正 * 负
if ( a[ i ] >= 0 ) { DP[ i – 1 , 1 ] * a[ i ] } else { DP[ i – 1 , 0 ] * a[ i ] }
最后的值为 DP[ i , 0 ]
可优化的点:只需要保存前两项的值,可优化为 int[2][2],或者使用临时变量也可。
老师的举例的两个 Python 版本都挺好的,附上:这个符合课堂思路,同时比较妙,扩展性强。
需要解释的点:为什么还要和 num[i] 本身做比较呢?
原因:因为需要连续,和 num[i]对比,是一种处理手段。
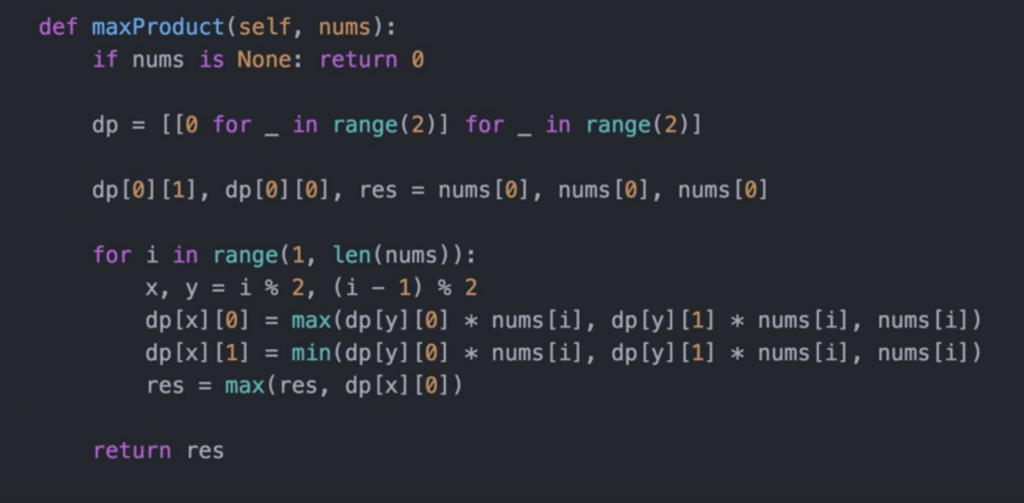
class Solution {
fun maxProduct(nums: IntArray): Int {
if (nums.isEmpty()) return 0
val dp = Array(2) {
IntArray(2) { nums[0] }
}
var res = nums[0]
for (i in 1 until nums.size) {
//动态下标
val x = i % 2
val y = (i - 1) % 2
//获取正数 max
dp[x][0] = Math.max(Math.max(dp[y][0] * nums[i], dp[y][1] * nums[i]), nums[i])
//获取负数 -max
dp[x][1] = Math.min(Math.min(dp[y][0] * nums[i], dp[y][1] * nums[i]), nums[i])
res = Math.max(res, dp[x][0])
}
return res
}
}这个是老师找的评论区的一个比较直观/暴力的写法:
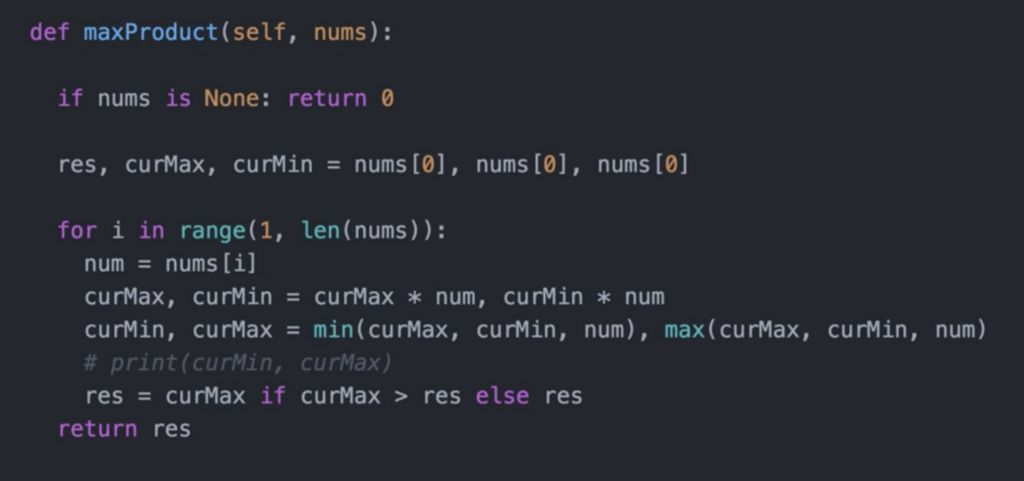

本站由以下主机服务商提供服务支持:
0条评论