开胃菜：

121. 买卖股票的最佳时机

特点：只能买一次，也只能卖一次

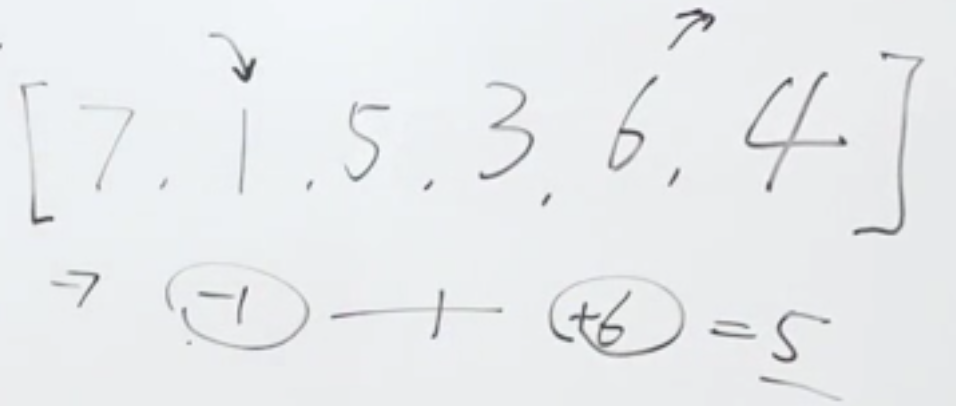
解法一：遍历

遍历时记录每次的最小值，同时和之前的最小值判断利润是否是最大，最大则记录下来，最后的全局最大值则是需要的答案

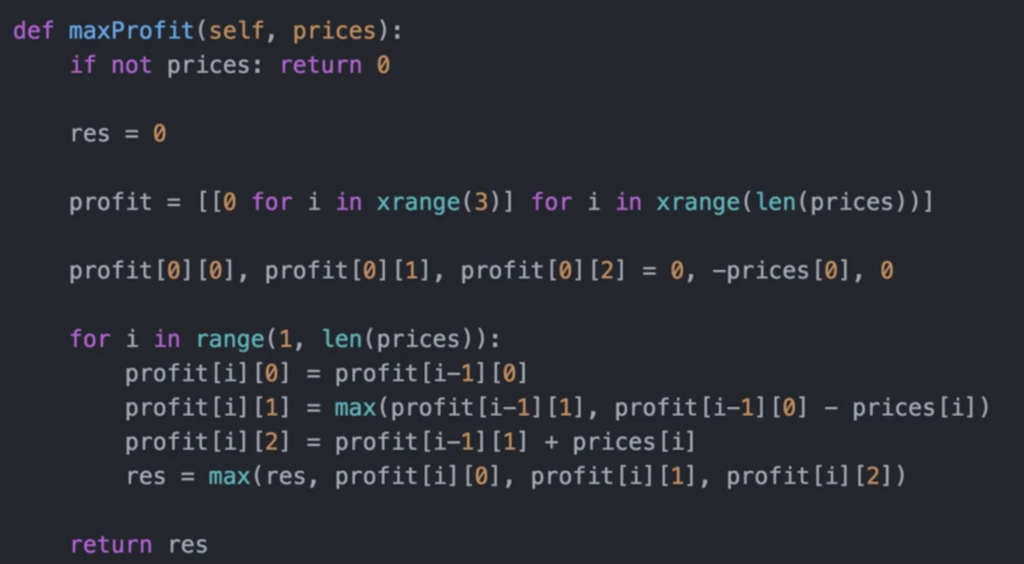
解法二：DP，动态规划

状态方程等定义看下半文。

122. 买卖股票的最佳时机 II

特点：可以买卖无数次

非动态规划解法：只要后一天的价格比前一天的价格高，那么就在前一天买进，后一天卖出即可。看之前的文章：点我

进阶：

123. 买卖股票的最佳时机 III

特点：总共只能买卖两次，二次买入时需先卖出

状态方程等定义看下半文。

188. 买卖股票的最佳时机 IV

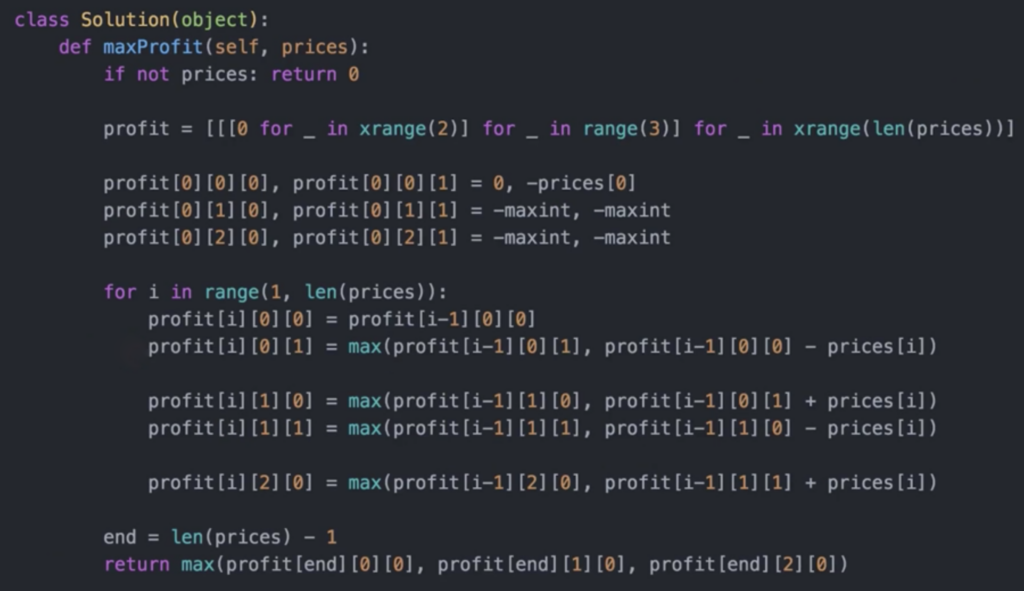
特点：最多进行 k 次交易

309. 最佳买卖股票时机含冷冻期

特点：有买卖冷却时间，类似股票中的 T + 1

714. 买卖股票的最佳时机含手续费

特点：有买卖手续费

关键解法：一个动态规划解决上述所有问题

共性：每次只能持有一股，需要解决的关键问题是 可以买卖 k 次

1. 状态定义：DP[i] 到第 i 天的 max profit（最大利润）,命名改为：MP[ i ]，结果 MP[ n – 1 ]
2. MP[ i ] 两个操作：
   买： MP[ i – 1 ] + ( – a[ i ] )
   卖： MP[ i – 1 ] + a[ i ]

但这样的状态无法判断当前是否持股，无法判断是买还是卖，所以还需要增加一个维度。状态重新定义为 MP[ i ][ j ] ，其中 j 可取值：
0 – 没有持有股票，可买
1 – 持有股票，可卖

此时的状态方程：

但这样的状态无法判断当前交易了多少次，所以还需要定义一维用于表示之前交易了多少次。状态重新定义MP[ i ][ j ][ k ]，i 代表天数，j 代表是否持有了股票， k 代表总共交易了多少次，所以现在变成了一个三维问题。

为了方便，换个顺序：MP[ i ][ k ][ j ]

时间复杂度：O(N * K * 2) = O( N * K) ，空间复杂度与时间复杂度相同。
N代表 n 天，K 表示最多 k 次交易，2 为是否持有股票。

此时的状态方程：结果：max { MP[n – 1 , {0 .. k} , 0] }
即：n -1 天中未持有股票的 MP 最大值

关于 Cool Down 的309题，可将第二维 k，改为记录是否为冷冻状态，取值：
0 – 之前交易了处于冷却状态
1 – 未交易，或者过了冷却时间，处于可交易状态

状态方程与上述类似，但是比 k 更简单一点，因为只需要判断是否是 cool down 状态。

如果再加深一下印象，可以买多股 x 的状态：将第三维 j 改写为范围0到 x 的持有股数。

时间复杂度：O(N * K * X) = O( N * K * X) ，空间复杂度与时间复杂度相同。
N代表 n 天，K 表示最多 k 次交易，X代表持有 x 股。

白板：

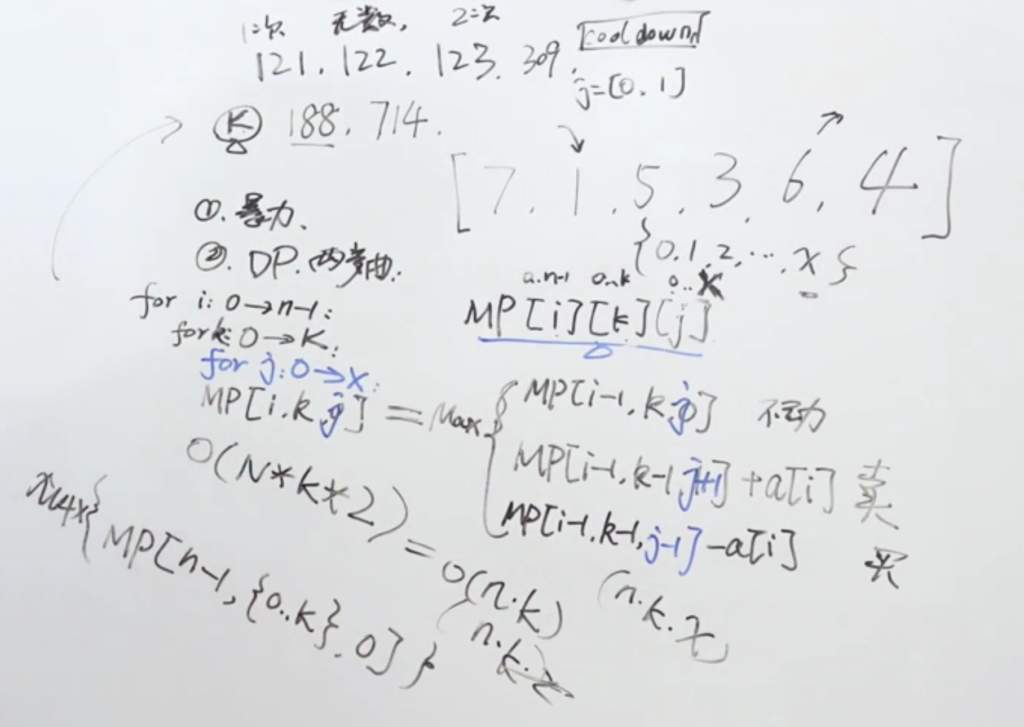
最终白板：老师说这是最复杂的情况，如果弄明白整个系列，面试中遇到类似问题基本上就迎刃而解了。

最终：老师并未给出所有解，此系列还是需要自己慢慢磨。