300. 最长上升子序列

解法一：暴力求解

剪枝：后面的要比前面的大，不然就不用继续查找了。

时间复杂度：O(2^n)

解法二：动态规划

可以发现最优子结构。

1. 状态定义：DP[ i ] 从头到 i 元素的最长子序列的长度
2. 状态转移方程：
   DP[ i ] = max { DP[ j ] + 1 } = max { DP[ j ] } + 1
   注：j ：0 -> i -1（j 必须是 i 的前置元素） 且 a[ j ] < a [ i ]

简单来说就是：当前的最长子序列 = DP[ 0 ] , DP[ 1 ] 到 DP[ n – 1 ] 中的最长子序列 + 1（包括当前元素）

最终结果就是： DP[ i ]

时间复杂度：O(N ²)

class Solution {
    fun lengthOfLIS(nums: IntArray): Int {
        if (nums.isEmpty()) return 0

        var res = 1
        val dp = IntArray(nums.size + 1) { 1 }

        for (i in 1 until nums.size) {
            for (j in 0 until i) {
                if (nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1)
                }
            }
            res = Math.max(res, dp[i])
        }
        return res
    }
}

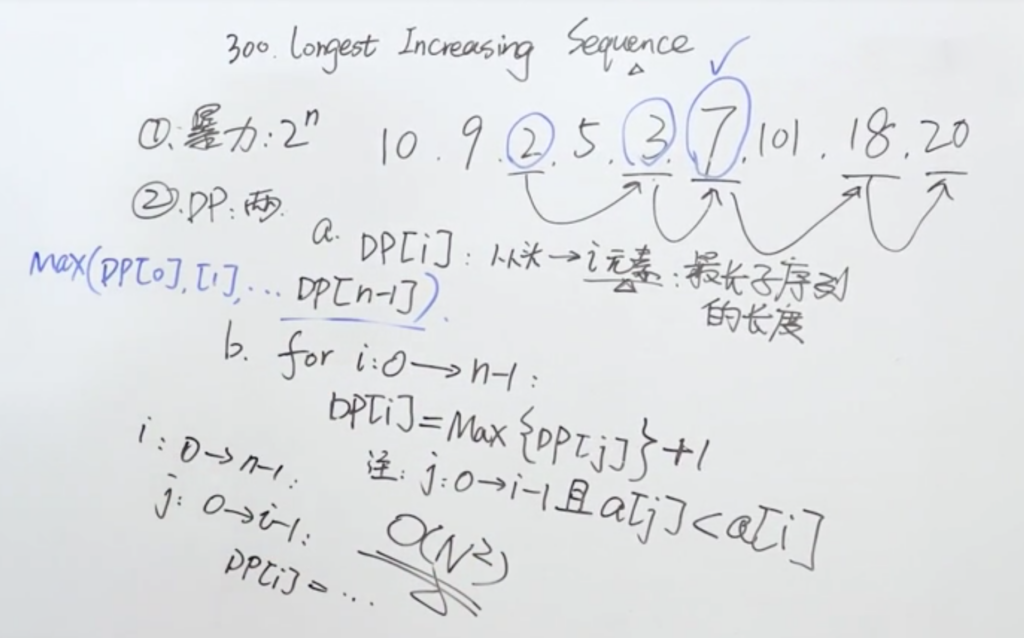
解法三：二分法

优化第二个循环，维护一个数组，使用二分法进行维护。

可行原因：最长子序列的顺序是上升的

细节：使用二分法判断新进入的元素与已知的子序列最后一个元素的关系，如果比最后一个小，就把最后一个换掉，如果比最后一个大，则加入这个元素。

数组变化过程大概如此:

例： 10 9 2 5 3 7 101 18 20

10       初始值
9        新进入元素9 比之前的10 小，替换掉10
2        2比之前的9小，替换掉9
2 5      5比2大，直接加入
2 3      3比5小，替换5
2 3 7    依次循环往返
2 3 7 101
2 3 7 18
2 3 7 18 20

时间复杂度：(N * logN)

C++版：