解法一:暴力
枚举每个面额,看需要走多少次。递归判断可行路径。从最大的开始枚举,返回总面额 count 最小的。
时间复杂度:O(2^n)
解法二:贪心 行不通
解法三:DP
- 状态定义:DP[ i ] 拼成面值 i 的最少次数
- 转换转移方程:
DP[ i ] = min { DP[ i – coins[j] ] } + 1
+ 1表示本身需要走一步,coins 代表几种面额,j 范围:0 到 n -1,i 代表需要拼的面值
简单来说:拼成面值 i 的最少次数 = 拼成[面值 i – 几种面额大小]面值中的最少步数 + 1
最终结果就是 DP[ x ],x 为需要拼凑的面值。
边界条件:DP[0] = 0,选择面额时,面额本身不能大于需要拼凑的面值
时间复杂度: O(0..x 面值 * 可选面额种类) = O(X * N)
空间复杂度:一维数组 O(X)
class Solution {
fun coinChange(coins: IntArray, amount: Int): Int {
val max = amount + 1
val dp = IntArray(max) { max }
dp[0] = 0
for (i in 1..amount) {
for (j in coins.indices) {
if (coins[j] <= i) {
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1)
}
}
}
return if (dp[amount] > amount) {
-1
} else {
dp[amount]
}
}
}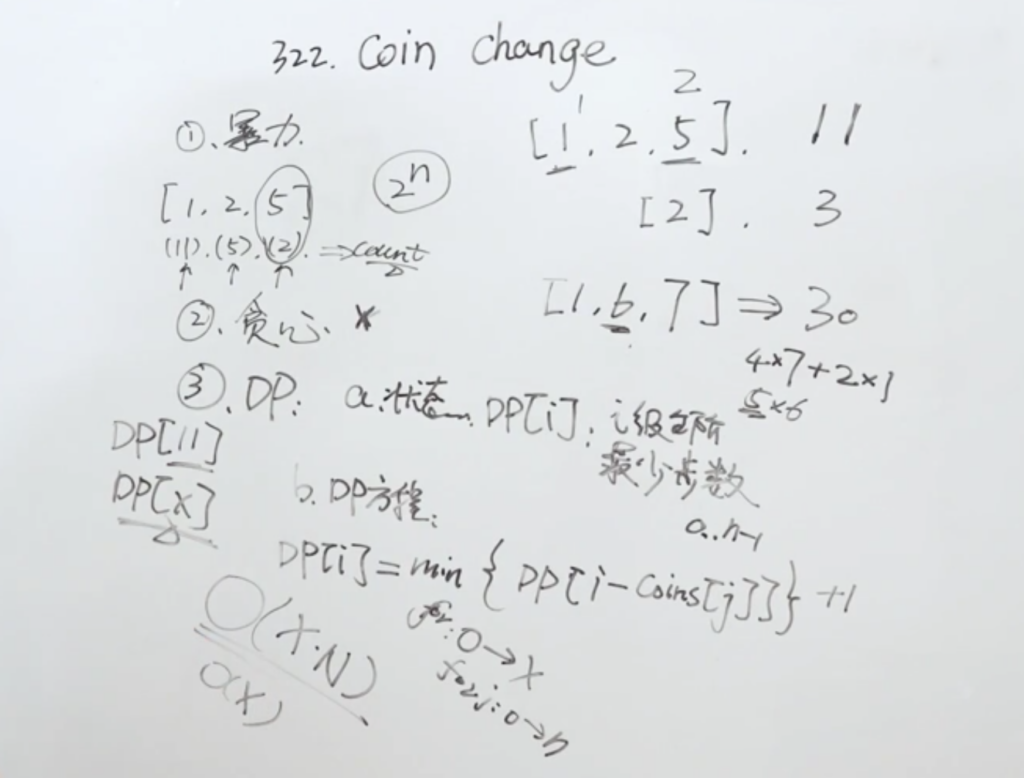
本站由以下主机服务商提供服务支持:
0条评论