题：输入某二叉树的前序和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如，输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建并输出头结点，二叉树定义如下：

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
}

解法：递归，原理如下图：想的是否想简单一点，然后再用递归思想处理

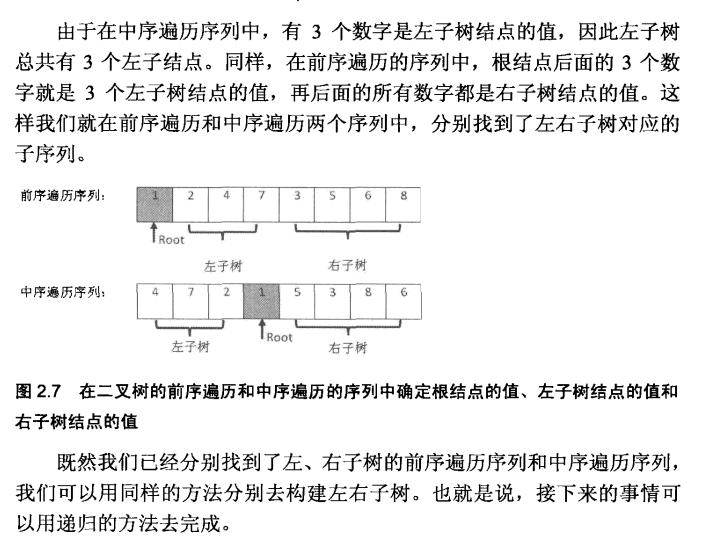
代码：

/**
 * 递归重构二叉树
 * @param pre 先序遍历
 * @param in 中序遍历
 * @return 完成后的新二叉树
 */
public static TreeNode reConstructBinaryTree(int[] pre, int[] in) {
    return constructCore(pre, 0, pre.length - 1, in, 0, in.length - 1);
}

/**
 * 递归主要逻辑
 * @param pre 先序遍历
 * @param startPreOrder 先序遍历起始点
 * @param endPreOrder 先序遍历终点
 * @param in 中序遍历
 * @param startInOrder 中序遍历起始点
 * @param endInOrder 中序遍历终点
 * @return 当前重构后的节点
 */
private static TreeNode constructCore(int[] pre, int startPreOrder, int endPreOrder, int[] in, int startInOrder, int endInOrder) {
    //前序遍历的起点是根节点的值
    int rootValue = pre[startPreOrder];
    TreeNode root = new TreeNode();
    root.val = rootValue;
    root.left = root.right = null;
    //如果只有一个节点
    if (startPreOrder == endPreOrder) {
        if (startInOrder == endInOrder && pre[startPreOrder] == in[startInOrder]) {
            //中序遍历起始位置等于结尾位置 并且这两个位置的值相等
            return root;
        } else {
            //否则不合法 返回null
            return null;
        }
    }
    //在中序遍历中找到根节点的值 rootInOrder为中序遍历中根节点的位置
    int rootInOrder = startInOrder;
    while (rootInOrder <= endInOrder && in[rootInOrder] != rootValue) {
        ++rootInOrder;
    }
    if (rootInOrder == endInOrder && in[rootInOrder] != rootValue) {
        //中序遍历头尾位置相同 且找到的根节点值与根节点不一致 则认为不合法 返回null
        return null;
    }

    int leftLength = rootInOrder - startInOrder;
    int leftPreOrderEnd = startPreOrder + leftLength;

    if (leftLength > 0) {
        //构建左子树
        root.left = constructCore(pre, startPreOrder + 1, leftPreOrderEnd, in, startInOrder, rootInOrder - 1);
    }
    if (leftLength < endPreOrder - startPreOrder) {
        //构建右子树
        root.right = constructCore(pre, leftPreOrderEnd + 1, endPreOrder, in, rootInOrder + 1, endInOrder);
    }
    return root;
}

测试主函数加递归输出新二叉树的先序遍历 ：

public static void main(String[] args) {
    int[] pre = {1, 2, 4, 7, 3, 5, 6, 8};
    int[] in = {4, 7, 2, 1, 5, 3, 8, 6};
    preOrderTraverse(reConstructBinaryTree(pre, in));
}

/**
 * 递归先序遍历
 * @param root root节点
 */
public static void preOrderTraverse(TreeNode root) {
    if (root != null) {
        System.out.print(root.val + " ");
        preOrderTraverse(root.left);
        preOrderTraverse(root.right);
    }
}

但是书中表达的判断逻辑还是有点多，不方便快速记忆和理解，可解除一些限定范围：

    private static TreeNode constructCore(int[] pre, int startPreOrder, int endPreOrder, int[] in, int startInOrder, int endInOrder) {
        if (startPreOrder>endPreOrder||startInOrder>endInOrder){
            return null;
        }
        //前序遍历的起点是根节点的值
        int rootValue = pre[startPreOrder];
        TreeNode root = new TreeNode();
        root.val = rootValue;
//        root.left = root.right = null;
        //如果只有一个节点
//        if (startPreOrder == endPreOrder) {
//            if (startInOrder == endInOrder && pre[startPreOrder] == in[startInOrder]) {
                //中序遍历起始位置等于结尾位置 并且这两个位置的值相等
//                return root;
//            } else {
                //否则不合法 返回null
//                return null;
//            }
//        }
        //在中序遍历中找到根节点的值 rootInOrder为中序遍历中根节点的位置
        int rootInOrder = startInOrder;
        while (rootInOrder <= endInOrder && in[rootInOrder] != rootValue) {
            ++rootInOrder;
        }
//        if (rootInOrder == endInOrder && in[rootInOrder] != rootValue) {
            //中序遍历头尾位置相同 且找到的根节点值与根节点不一致 则认为不合法 返回null
//            return null;
//        }

        int leftLength = rootInOrder - startInOrder;
        int leftPreOrderEnd = startPreOrder + leftLength;

//        if (leftLength > 0) {
            //构建左子树
            root.left = constructCore(pre, startPreOrder + 1, leftPreOrderEnd, in, startInOrder, rootInOrder - 1);
//        }
//        if (leftLength < endPreOrder - startPreOrder) {
            //构建右子树
            root.right = constructCore(pre, leftPreOrderEnd + 1, endPreOrder, in, rootInOrder + 1, endInOrder);
//        }
        return root;
    }

最终精简版：

private static TreeNode constructCore(int[] pre, int startPreOrder, int endPreOrder, int[] in, int startInOrder, int endInOrder) {
    if (startPreOrder > endPreOrder || startInOrder > endInOrder) {
        return null;
    }
    //前序遍历的起点是根节点的值
    int rootValue = pre[startPreOrder];
    TreeNode root = new TreeNode();
    root.val = rootValue;

    //在中序遍历中找到根节点的值 rootInOrder为中序遍历中根节点的位置
    int rootInOrder = startInOrder;
    while (rootInOrder <= endInOrder && in[rootInOrder] != rootValue) {
        ++rootInOrder;
    }

    int leftLength = rootInOrder - startInOrder;
    int leftPreOrderEnd = startPreOrder + leftLength;

    //构建左子树
    root.left = constructCore(pre, startPreOrder + 1, leftPreOrderEnd, in, startInOrder, rootInOrder - 1);
    //构建右子树
    root.right = constructCore(pre, leftPreOrderEnd + 1, endPreOrder, in, rootInOrder + 1, endInOrder);
    return root;
}

以上，应该还是比较好理解的。